ถ้าคุณอ่านชื่อเรื่องแล้วเข้าใจทันทีว่าหมายความว่าอะไร คุณต้องมีปัญหาคาใจอยู่แน่ๆ
เรื่องบางเรื่องไม่จำเป็นต้องรู้ แต่ไม่รู้ก็ค้างคาใจ
บางเรื่องก็คาใจมาเป็นสิบปี
อย่างเช่นว่า ทำไมสูตรค่าเบี่ยงเบนมาตรฐาน (standard deviation) ของประชากร (population) เอาความแปรปรวนไปหาร N แล้วถอดรูท แต่สูตรค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง (samples) ใช้ n-1 แทน
จะทำเป็นลืมๆ ไปก็ไม่ได้ เพราะทุกครั้งที่คำนวณค่าความเบี่ยงเบน Excel ก็จะย้ำเตือนด้วยตัวเลือก STDEV, STDEV.P และ STDEV.S
เหมือนจะท้าทายเราว่า รู้แน่เหรอว่ากำลังทำอะไรอยู่
ถ้าคุณเป็นนักเรียนดีเด่นฉบับไทย คุณจะจดจำได้ว่า อ๋อ ที่เราใช้ n-1 แทน N ก็เป็นเพราะต้องปรับแก้เรื่อง degree of freedom
แปลว่าอะไรเหรอ…
แน่นอนว่าเราสามารถพิสูจน์ได้ด้วยคณิตศาสตร์ว่าทำไมต้องใช้ n-1 แทน N ในสูตรค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง แต่…
วันนี้เราจะมาดูกันให้เห็นจะจะว่าทำไม
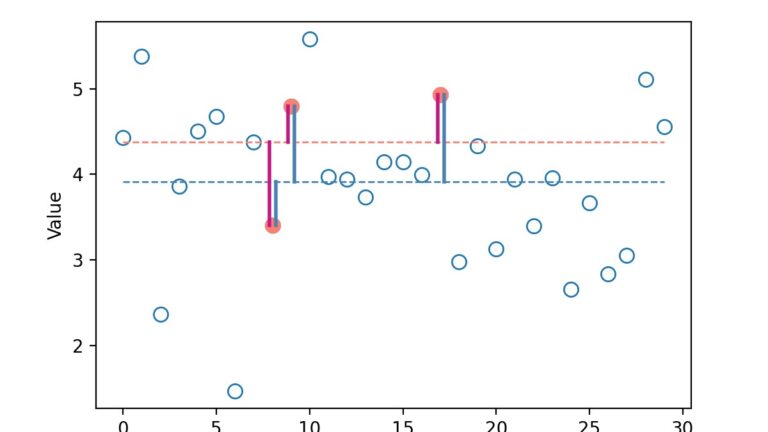
สมมติว่าเรามีประชากร 30 ตัว (N=30) โดยที่ข้อมูลของประชากรแต่ละตัวมีค่าต่างกันไปตามรูปด้านล่าง

วิธีหาค่าเบี่ยงเบนของประชากรก็แค่ เอาระยะห่างระหว่างข้อมูลของแต่ละคน กับ ค่าเฉลี่ยประชากร (เส้นสีน้ำเงินในรูปด้านล่าง) มายกกำลังสอง แล้วนำผลที่ได้มารวมกัน หาร N แล้วถอดรูท
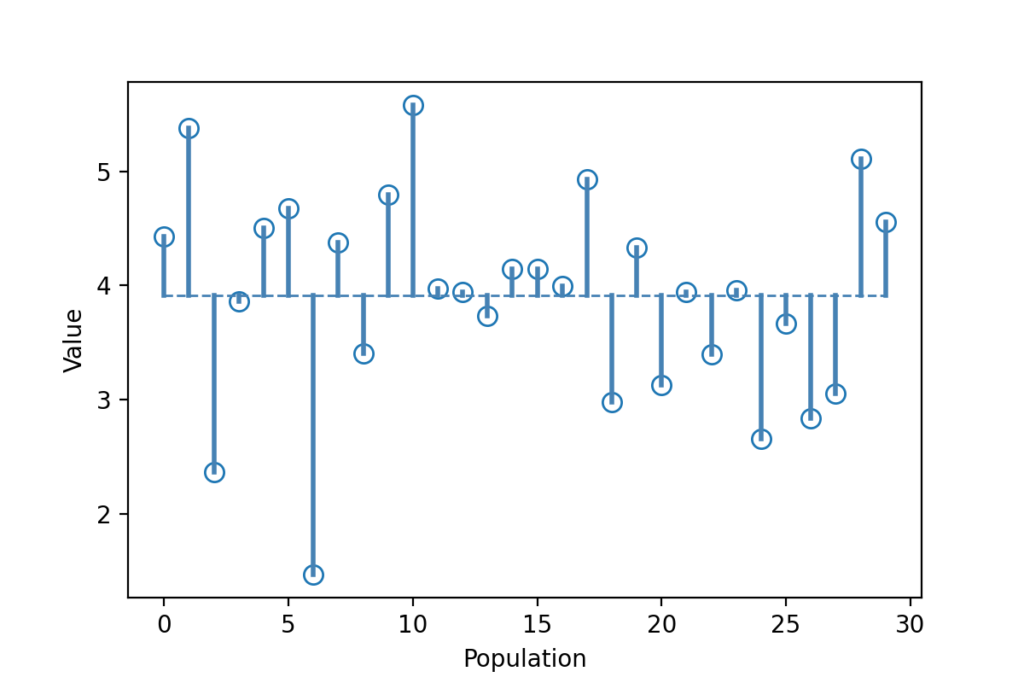
ถ้าเราเก็บข้อมูลของประชากรได้ทุกคน ก็คำนวณค่าเบี่ยงเบนประชากรไปเลยครับ ถูกต้องที่สุด
แต่ในหลายกรณีที่ประชากรมีจำนวนมาก (เช่น หลายแสน) แล้วไม่สามารถเก็บข้อมูลได้ทั้งหมด เราก็จะเก็บข้อมูลจากกลุ่มตัวอย่างแทน
สมมติว่าเราเก็บตัวอย่างได้แค่ 3 ตัว (n=3) ตามจุดสีแดงในรูปด้านล่าง
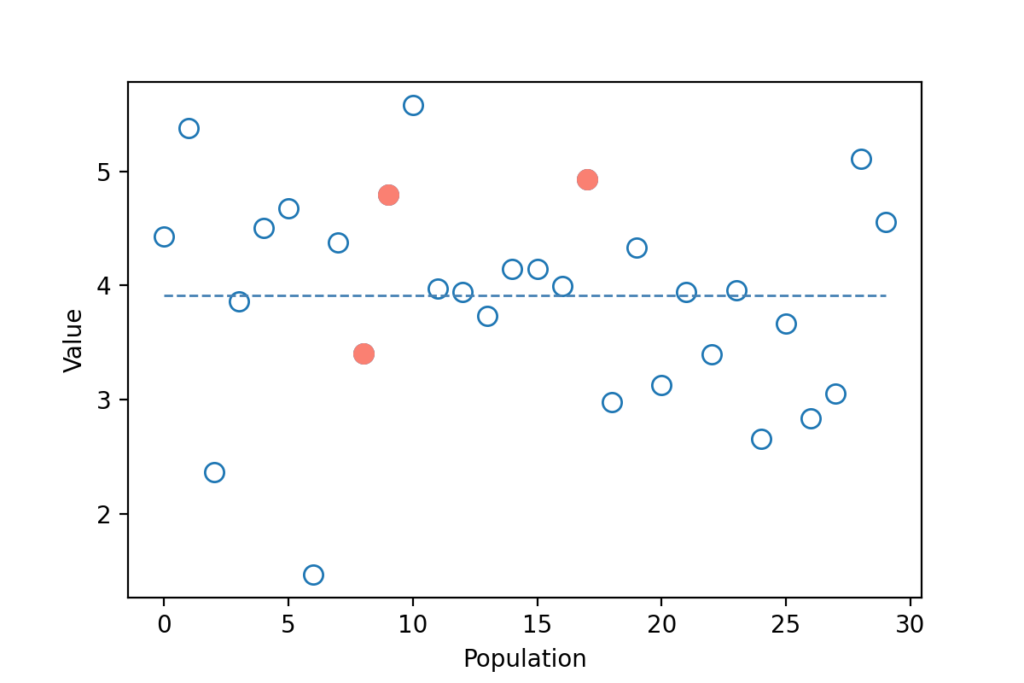
เวลาที่จะหาค่าเบี่ยงเบนมาตรฐาน เราจะต้องใช้ระยะห่างระหว่างข้อมูลของแต่ละคน กับ ค่าเฉลี่ยกลุ่มตัวอย่าง (เส้นสีแดงในรูปด้านล่าง) แทน เพราะเราไม่รู้ค่าเฉลี่ยประชากร
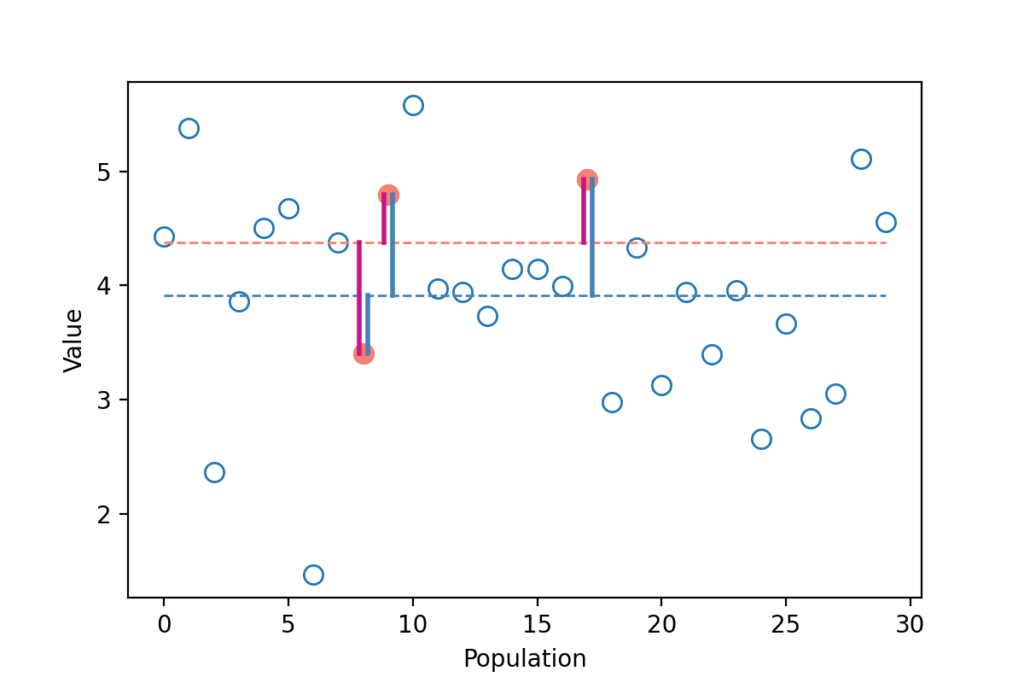
สังเกตไหมครับว่า
ผลรวมของระยะห่างกำลังสองของเส้นสีแดง (วัดจากค่าเฉลี่ยกลุ่มตัวอย่าง) น้อยกว่าของสีน้ำเงิน (วัดจากค่าเฉลี่ยประชากร)
บังเอิญหรือเปล่า?
ไม่ครับ จะสุ่มกี่ครั้งผลรวมของระยะห่างกำลังสองของเส้นสีแดง ก็น้อยกว่าสีน้ำเงินเสมอ
จะน้อยกว่ามาก หรือ น้อยกว่าไม่มาก ก็แล้วแต่ แต่ยังไงก็ต้องน้อยกว่า (หรือถ้าฟลุ๊คมากๆ ก็เท่ากัน)
ที่เป็นแบบนี้ก็เพราะว่า การวัดระยะจากค่าเฉลี่ยกลุ่มตัวอย่าง จะทำให้ผลรวมของระยะห่างกำลังสองน้อยที่สุด
ถึงตอนนี้คุณคงเดาได้แล้วว่า…
โดยเฉลี่ย ผลรวมของระยะห่างที่วัดจากค่าเฉลี่ยกลุ่มตัวอย่างยกกำลังสองจะน้อยไปเป็นสัดส่วน 1/n (อันนี้ต้องพิสูจน์ด้วยคณิตศาสตร์)เราเลยต้องปรับแก้ด้วยด้วยการคูณ n/(n-1) หรือใช้ n-1 ในสูตรค่าเบี่ยงเบนมาตรฐานนั่นเอง
หวังว่าจะทำให้สบายใจกันแล้วนะครับสำหรับเรื่อง n-1
ป.ล. ผมเผยแพร่บทความนี้ครั้งแรกบน medium